SIGNIFICANCE OF PREFERENTIAL FLOW IN ESTIMATING GROUNDWATER RECHARGE RATES WITH A SOIL WATER BALANCE MODEL IN THE DRY ZONE OF SRI LANKA
R. P. de Silva
Department of Agricultural and Plantation Engineering, The Open University, Nawala, Nugegoda, Sri Lanka
ABSTRACT
Percolation of rainwater through cracks, fissures and worm and root channels in the soil (preferential flow paths) are receiving increasing attention from scientists all over the world. A study was carried out to determine the significance of the preferential flow component in estimating recharge with a soil water budget. Though the evidence available suggest that preferential flow is likely, its effect on estimating recharge with a soil water budget was found to be not significant in the dry zone of Sri Lanka. However, it is safe to allow about 5% of rainfall as preferential flow so that estimates of recharge are likely to be more realistic.
INTRODUCTION
Groundwater recharge rate, which is defined as the rate at which the water table is replenished (during rainfall, irrigation or from seepage of surface water bodies), is the single most important parameter one needs to know in developing the groundwater resource. It is also important;
(a) as one of the important inputs (often with the largest uncertainty) into groundwater management models;
(b) in the studies of contamination and pollution of groundwater resources and determination of safe dumping sites for wastes;
(c) in the determination of stream and land salinisation due to an increase in recharge which could result from a change in land use. (e.g., with agriculture, short rooted crops replace deeply rooted woodlands resulting in higher recharge accompanied by increasing water tables accompanied by stream and land salinisation).
There are a number of methods of estimating recharge (Lerner et al, 1990; de Silva, 1996).
Of these, the soil water balance of the root zone, tracer techniques, numerical modelling of the unsaturated zone flow equation, use of Darcy’s law, use of lysimeters, water table fluctuation method, and the catchment water balance method are some of the more commonly used methods of estimating recharge (de Silva, 1996; de Silva, 1998). Many authors have discussed the relative merits and de-merits of each of these methods (Allison, 1994; de Silva, 1998). The soil water balance of the root zone is a method which can be applied in most situations under most climates and has been used widely throughout the world (except in very arid areas) to estimate the rates of recharge successfully.
In a soil water balance (also called a soil water budget), the recharge is estimated as the residual of all the other fluxes in the hydrological cycle. The principle being that all theses fluxes (i.e., precipitation, evapotranspiration, run off, interception and soil moisture changes) are usually relatively more easily measured or estimated than recharge. Therefore, considering a volume balance of water in the root zone the recharge (Re) is estimated from
![]()
where P is precipitation, I is interception of rainfall by vegetation, RO is run off, ETa is actual evapotranspiration and .S is change in soil moisture storage. If the balance is carried out annually (especially from the end of rainy season to the same time the following year; as the moisture content in the soil at both times will be at field capacity), the change in soil moisture storage is negligible. Therefore equation 1 reduces to;
![]()
In equation 2, the importance of preferential flow (i.e., the flow through cracks, fissures and root channels of the soil by passing the soil matrix) is not immediately clear as there is no such term in it. However, the same equation can be written as in equation 3, where the first term within brackets is the matrix flow (MF) and the second term within brackets is the preferential flow (PF).
![]()
Now, the estimation of actual evapotranspiration is affected by matrix flow, which in turn is affected by the amount of preferential flow. Therefore, estimates of recharge from a soil water budget method (which are affected by estimates of actual evapotranspiration), are affected as a result of preferential flow. Hence, preferential flow needs to be considered in using the soil water balance unless evidence is available to the contrary. Therefore, the objectives of this study were:
1. Review the use of preferential flow in estimating recharge with a soil water balance.
2. Determine the likelihood of occurrence of preferential flow in the dry zone of Sri Lanka.
3. Evaluate the importance of considering the preferential flow component in a soil water budget in the dry zone of Sri Lanka.
MATERIALS AND METHODS
The methodology adopted in achieving the objectives of this study are as follows:
(a). Review the research work on the use of preferential flow in estimating recharge with a soil water balance model.
(b). Select suitable study locations in the dry zone of Sri Lanka for determining if preferential flow is likely and also for determining the importance of considering the preferential flow in a soil water budget.
(c). Develop a suitable soil water budget model to estimate recharge in the dry zone which takes account of preferential flow. Also identify all soil, vegetation and climatic parameters and data required for the soil water budget.
(d). Identify the field data collection, field tests and field data observation necessary to determine if preferential flow is likely in the dry zone.
(e). By laboratory tests, field tests and field observations determine parameters and data in (c) and
(d) above.
(f). Determine the likelihood of the occurrence of preferential flow in the dry zone.
(g). Estimate recharge with and without preferential flow and compare the results.
Study locations
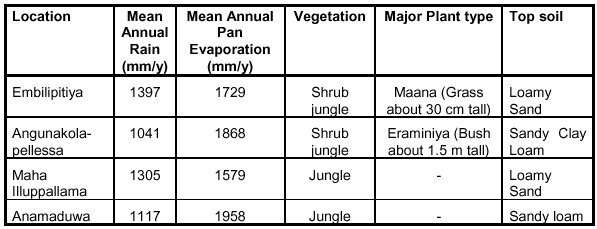
Study locations chosen in the dry zone of Sri Lanka (depending on the suitability for the present study, availability of data, accessibility and availability of personnel necessary to carry out daily field tests) are shown in Figure 1. Details of climate, soils and vegetation of each study location are given in Table 1.
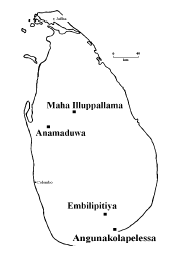
Fig. 1 - Study locations in the dry zone of Sri Lanka
Table 1: Physical details of study locations in Sri Lanka
Laboratory and field experiments
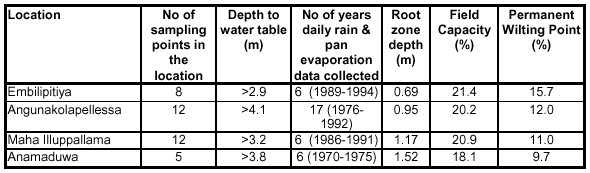
Under item (e) above the field capacity and permanent wilting point of the root zone at all the study locations were determined using a pressure plate apparatus. The depth of root zone at each location was also measured. Table 2 summarises the test results for all study locations. The auger holes drilled to obtain soil samples were extended to the water table (unless hard rock was encountered before hitting the water table) and piezometers were installed to measure the depth to the water table using a dipmeter. More details of all this soil parameters and climatic data and field experimentation are found in de Silva (1996).
Table 2: Summary of soil properties and vegetation parameters at each study location
and details of climatic data collected
Preferential flow - Literature Review
The occurrence of flow of water through preferred pathways (i.e., cracks and fissures in the soil, worm and root channels and unstable wetting fronts called fingering in more coarse textured soils) has been observed as far back as in 1882 (Germann and Beven, 1981). It is now known that such flow can occur through the whole spectrum of soils. Since the dry zone of Sri Lanka contains more fine textured soils than coarse textured ones, more emphasis in this paper will be put on preferential flow through fine textured soils (i.e., through clays, silts and clay loams etc).
Germann and Beven (1981) define the boundary between macropore and micropore as about 1.5 mm diameter (depending on the surface tension, temperature and density of water).
There are recorded instances of macropore flow occurring up to 10 m depth in loess soil (Beven and Germann, 1980), and > 20 m in sandy soils (Sharma and Hughes, 1985).
Table 3 Models to estimate flow through preferred paths shows some instances where
workers have attempted to estimate this flow by various models.
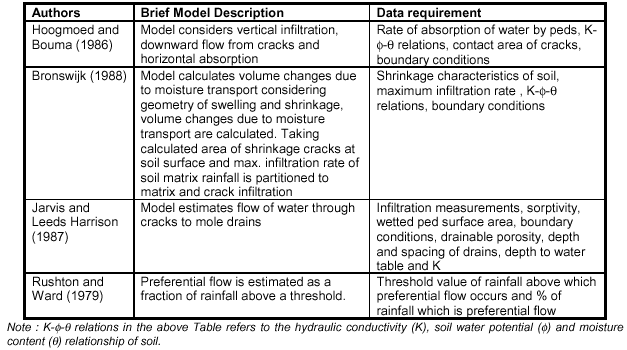
Table 4 shows some recorded instances of using a soil water balance to estimate recharge. As seen from Table 4, only Rushton and Ward (1979) have considered the preferential flow as a component in the soil water balance. It must be noted here that, for preferential flow to be important (from the point of view of a soil water budget), it is not necessary for these paths to be deep, as the amount of water by passing the soil matrix, even though small, may affect actual evapotranspiration, and hence recharge.
Soil water budget model
The soil water balance model formed to estimate groundwater recharge is shown in Figure 2. A detailed explanation of the soil water balance model is given in de Silva (1996) with an explanation of the spreadsheet model used for the calculations.
As seen from Figure 2, parameters of rainfall interception storage capacity (Isc), Runoff threshold (ROt), runoff coefficient (ROc), Preferential flow threshold (PFt), Preferential flow coefficient (PFc) and root constant (RC) for a particular location are required for the soil water balance model. Table 5 shows the values of these parameters obtained by considering the vegetation, rainfall distribution and soil types at each location. A detailed explanation of obtaining these parameters for each location is given in de Silva (1996).
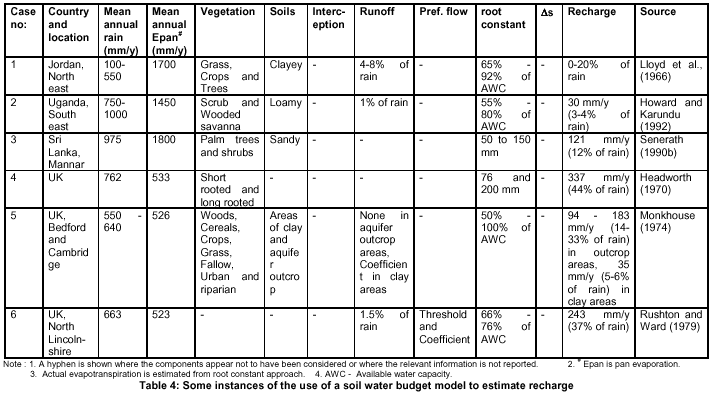

Fig. 2 Flow chart of the soil water balance model to estimate soil moisture deficit
Table 5 Likely model parameters for different study locations in Sri Lanka
RESULTS AND DISCUSSION
Determination of the likelihood of preferential flow in the dry zone.
The following factors suggest that preferential flow at least in the shallower depths is likely:
(a) Figure 3, which shows the plots of soil moisture deficit and groundwater level with time for Embilipitiya, indicate that at least on a few days (2-6 April and 25 July indicated by arrows in Fig. 3), the water table rose when a soil moisture deficit existed.
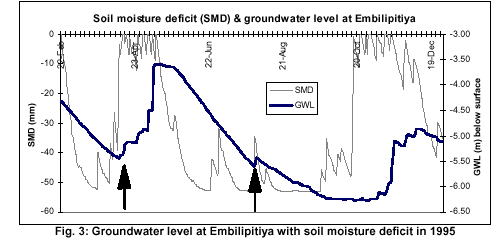
The possibility of rainwater infiltrating along the casing of the piezometer could cause an apparent water table rise soon after a rainfall event. However, the casing outside was carefully refilled and a depth of about 0.5 m from the surface was filled with impermeable clay (and also the surface covered with cement mortar). Therefore, it is unlikely that any preferential flow paths were present along the outside of the casing causing a water table rise during periods where a soil moisture deficit existed. It is also possible to have a rise in water table due to other reasons like water well recovery after pumping and regional groundwater flow. However, for the period concerned, there was no pumping and the water levels from other piezometers (de Silva, 1996) suggest that the water table was flat and therefore, it is likely that the water level rise when a soil moisture deficit existed was caused by preferential flow.
(b) The soils found in the dry zone are more clayey than sandy and structured clayey soils are more likely to have preferential flow, through cracks which often remain open even when wetted.
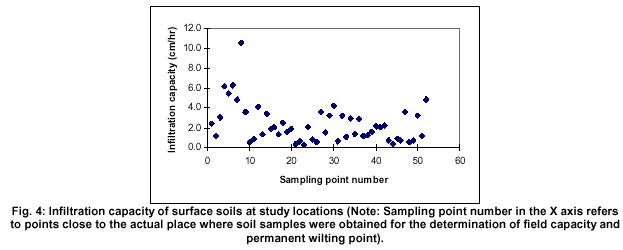
(c) Some of the values of infiltration rates (Figure 4) are rather high for the textures encountered, which may be due to the presence of preferential flow paths. These infiltration rates were measured using the concentric ring infiltrometers and full details of experimental procedure and results are given in de Silva (1996).
Estimates of recharge from the soil water balance
Table 6 shows the estimates of recharge with different amounts (0%, 1%, 5%, 10%, 15% of rainfall) of preferential flow allowed. As seen from Table 6, the difference between these estimates are small for Embilipitiya and Maha Illuppallama [with coefficient of variation (CV) being 3.8% and 7.6% respectively] and slightly higher for Angunakolapellessa and Anamaduwa (19.1% and 13.8% respectively). From Table 2, it is seen that Embilipitiya and Maha Illuppallama have higher mean annual rainfall and less mean annual pan evaporation than the other two locations.
Therefore, it appears that in locations where climate is comparatively wet, the significance of preferential flow in estimating recharge with a soil water budget is comparatively less.
Table 6 Estimates of Recharge (in mm/y) for 0%, 1%, 5%, 10% and 15% preferential flow
coefficient at different study locations in the dry zone of Sri Lanka

In comparing the effect of different amounts of preferential flow, not only total annual values of recharge need to be compared, but also the distribution of recharge with time need to be compared to see if all the models produce a similar result (i.e., comparing only the annual values of recharge is not sufficient). Figures 5 and 6 show the distribution of recharge and rainfall over a period of one year for Embilipitiya and Angunakolapelessa respectively with different amounts of preferential flow (similar graphs were obtained for Maha Illuppallama and Anamaduwa). An analysis of variance test can be carried out to see if these distribution are significantly different or not objectively (Gomez and Gomez, 1976).
Tables 7 shows the results of analysis of variance tests to see if distributions of recharge estimates are significantly different or not at Angunakolapellessa. In this test the daily estimates of recharge for one year were considered. Here again, the distributions at each location are significantly not different at 5% as Fcalc (calculated F statistic) is less than Fcrit (critical F static tabulated for 5% significance and 4 degrees of freedom) in Table 7 (Gomez and Gomez, 1976).
Similar results are obtained for other locations as well (with Fcalc and Fcrit respectively of 0.22, 2.37 for Embilipitiya, 0.27, 2.37 for Maha Illupallama and 0.61, 2.37 for Anamaduwa).
Table 7 Analysis of variance test results for comparing estimates for Angunakolapelessa

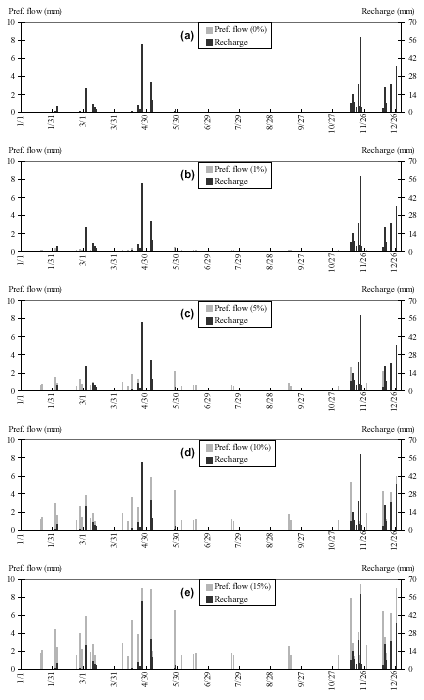
Fig. 5: Estimates of recharge and preferential flow (in 1989) for different amounts of preferential flow coefficient
for Embilipitiya
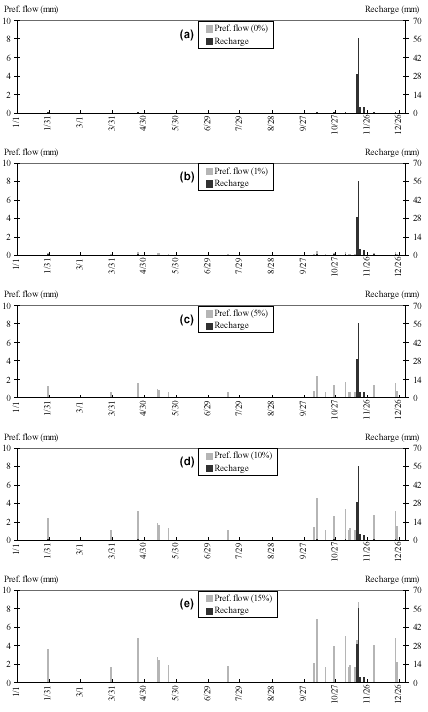
Fig. 6: Estimates of recharge and preferential flow (in 1976) for different amounts of preferential flow coefficient
for Angunakolapellessa
(3). The difference between considering and not considering preferential flow increases with the dryness of the area and unless specific information is available, about 5% of rainfall may be considered as the preferential flow component in the dry zone of Sri Lanka for more realistic estimates of recharge.
(4). More research work on preferential flow is required in order to understand both the mechanism and magnitude of it, so that the estimates of recharge are likely to be more realistic, which will have far reaching economic implications.
REFERENCES
Allison, G. B., Gee, G. W. and Tyler, S. W., (1994). Vadose-Zone Techniques for Estimating Groundwater Recharge in Arid and Semiarid Regions. Soil Science Society of America Journal, 58: 6-14.
Beven, K and Germann, P., (1980). The Role of Macropores in the Hydrology of Field Soils. Report no: 69, Institute of Hydrology, UK.
Bronswijk, J. J. R., (1988). Modelling of Water Balance, Cracking and Subsidence of Clay Soils. Journal of Hydrology, 97: 199-212.
De Silva, R. P., (1996). Estimating Groundwater Recharge in the Dry Zone of Sri Lanka with Special Emphasis on Spatial Variability. Unpublished PhD Thesis, Silsoe College, Cranfield University, UK.
De Silva, R. P., (1998). A review of the methods of estimating groundwater recharge in relation to the dry zone of Sri Lanka. The Open University Review of Engineering Technology Journal, Vol : 4(2): 3-12, Open University of Sri Lanka.
Germann, P. and Beven, K., (1981). Water Flow in Soil Macropores 1. Experimental Approach. Journal of Soil Science, 32: 1-13.
Gomez , K. A. And Gomez, A. A., (1976). Statistical Procedures for Agricultural Research (2 nd edition). John Wiley and Sons, New York.
Headworth, H. G., (1970). The Selection of Root Constants for The Calculation of Actual Evaporation and Infiltration for Chalk Catchments. Journal of Institution of Water Engineers, 24: 431-446.
Howard, K. W. F. and Karundu, J., (1992). Constraints on the Exploitation of Basement aquifers in East Africa - Water Balance Implications and the Role of the Regolith. Journal of Hydrology, 139: 183-196.
Hoogmoed, W. B. and Bouma, J., (1986). A Simulation Model for Predicting Infiltration into Cracked Clay Soil. Soil Science Society of America Journal, 44: 458-461.
Jarvis, N. J. and Leeds-Harrison, P. B., (1987). Modelling Water Movement in Drained Clay Soil. 1. Description of the Model, Sample Output and sensitivity. Journal of Soil Science, 38: 487-498.
Lerner, D. N., Issar, A. S. and Simmers, I., (1990). Groundwater Recharge : A Guide to Understanding & Estimating Natural Recharge. International Association of Hydrogeologists, Hannover.
Lloyd, J. W., Drennan, D. S. H. and Bennell, B. M. U., (1966). A Groundwater Recharge Study in North Eastern Jordan. Proceedings of Institution of Civil Engineers, 35: 615-631.
Monkhouse, R. A., (1974). An assessment of the groundwater resources of the lower Greensand in the Cambridge - Bedford Region. Water Resources Board, Reading, UK.
Rushton, K. R. and Ward, C., (1979). The Estimation of Groundwater Recharge. Journal of Hydrology, 41: 345-361.
Senerath, D. C. H., (1990b). Two case studies in estimation of groundwater recharge. Groundwater Monitoring & Management, IAHS Publication no.173, UK.
Sharma, M. L. and Hughes, M. W., (1985). Groundwater Recharge Estimation Using Chloride, Deuterium and Oxygen-18 Profiles in the Deep Coastal Sands of Western Australia. Journal of Hydrology, 81: 93-109.